遵义高考复读辅导班

面授小班

￥详询

416人看过

遵义启睿教育

白天班、晚班、周末班等7个班级

介绍

地址

相册

评价

学校

【课程内容】

根据学生的实际情况，普遍都是基础很薄弱，通过复习，主要让学生掌握基础分，选择填空6-8道（30-40分），17题统计概率（8-12分），18题数列或者解三角形首问)(6-8分），19题空间几何首问（6分），22题参数方程首问（3-5分），围绕这个目标进行三轮复习。

首先，先让学生掌握基础小题必会专题，集合的运算.复数的运算，命题，线性规划.数学文化.统计小题.平面向量.流程图共8个小专题，在高考中都是以基础题形式出现，让学生掌握6道。

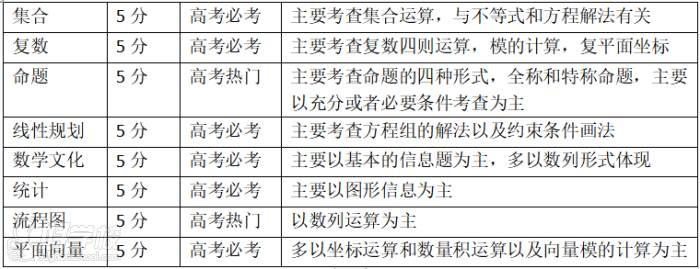
通过这部分基础专题复习，让学生掌握6道小题30分左右。

其次，函数部分基础小题，主要以函数的图像，零点问题，指数对数的运算多以比较大小，函数的求值（分段函数，对数运算），高考从四个部分选择一部分考查，属于基础偏中等题，主要让一部分学生掌握(5分）

然后就是客观大题部分：

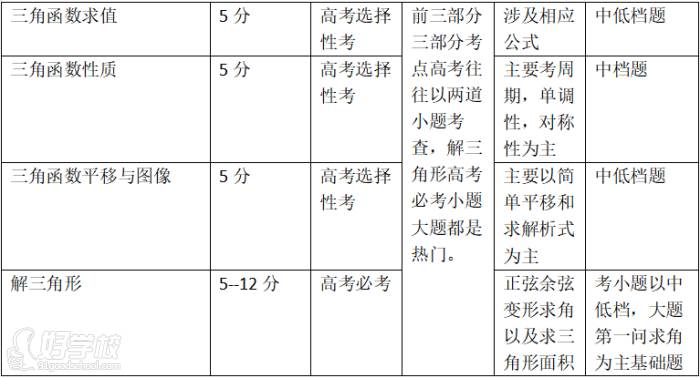
首部分，是三角函数和数列在高考中考22分，一道大题和两道小题，多以中低档题为主，大题以18或者19题体现，小题一道基础，一道中等。主要让学生掌握一道小题部分和大题首问，需要让学生掌握10分左右，在高考中具体考点和分值如下：

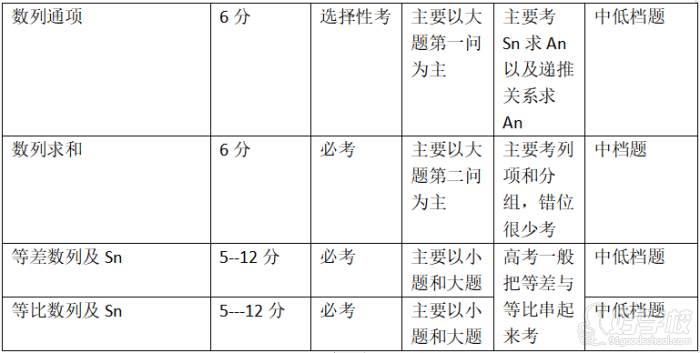
第二部分，是统计与概率部分大题，高考中占17分左右，一个小题和大题17题出现，最近三年高考统计与概率都是以基础题为主，主要考查学生的运算能力，必须要学生掌握的基础专题.主要考查抽样，样本估计总体（频率直方图，茎叶图，线性回归，独立性检验），最近几年高考都是以独立性检验和频率直方图为主。概率主要考查古典概率和几何概率，古典以小题和大题第二问出现，几何概率以小题出现，多以面积和长度类型的概率.要求学生掌握10-12分左右

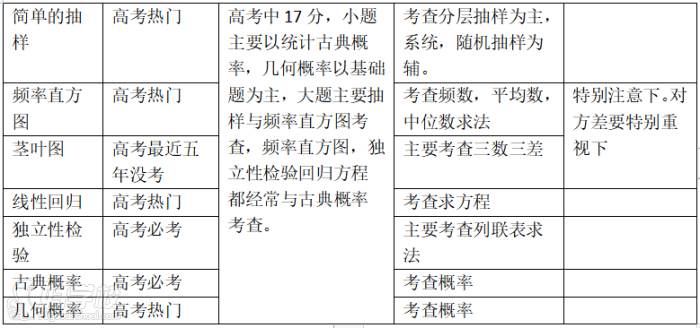
第三部分，也是中低档题型，在高考中22题，考查参数方程和极坐标方程，主要涉及到方程的转化，以及直线与曲线的交点.弦长.距离问题处理，与直线，圆.椭圆.抛物线相关知识有联系，这这一部分只需要学生学会转化方程，以及一些基础的弦长和距离的相关知识，需要学生掌握3----5分即可。

第四部分，空间几何部分，在高考占17分，一个小题加一个大题位于18或者19题，小题主要考查三视图或者球的问题，大题主要考查直线，平面之间的位置关系（平行，垂直为主），以及点到平面的距离和体积为主，复习这块主要让学生学会平行，垂直的证明，还要会一些最基本的外接球模型题，三视图等，让学生掌握6-10分左右。

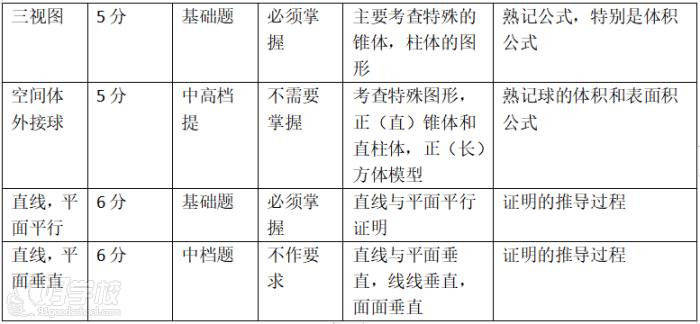
通过这些专题复习，高三共分为三轮复习，首轮全面复习基础知识，课上讲，课后练，每周小检测，两周阶段性小测，三周一综合测试，第二轮主要以板块复习，首先复习大题部分，统计与概率，三角函数与数列首问，空间几何首问，参数方程首问，小题特训采用7个选题加两个填空复习，每周都用限时周考，选择填空45分钟，大题60分钟。第三轮为综合冲刺训练

根据这个计划，一轮复习（2022.7-2023.2月中旬）的教学安排分为三个层次：

（1）试听课部分（数列部分）

（2）必备基础小题部分

（3）基础大题专题

（4）选讲部分（函数部分）

首部分：试听课部分

一周试听课：

（1）不等式的解法（单型）

（2）不等式解法（异侧双型）

（3）不等式解法（同侧双型）

（4）方程的解法：过渡下一元一次方程，分式方程，重点讲一元二次方程

（5）方程组解法：二元一次方程组，二元二次方程组解法

第二部分：基础小题部分

1.集合的运算

2.复数的运算

3.命题

4.流程图

5.不等式解法（一元二次不等式，分式不等式解法）

6.线性规划

7.平面向量运算

8.数学文化

9.函数的图像

第三部分：基础大题部分

（一）三角函数与解三角形部分

1.三角函数的求值

2.诱导公式

3.二倍角，和差公式求值

4.三角函数的性质（基础型）

5.三角函数图像与平移

6.解三角形（正弦，余弦定理，面积，周长求法）

（二）数列专题部分

1.一般数列的通项求法

2.等差数列及求和

3.等差数列及求和

4.一般数列的求和

（三）统计与概率部分：

1.简单的抽样

2.样本估计总体（频率直方图，茎叶图）

3.线性回归方程

4.独立性检验（列联表）

5.随机事件概率

6.古典概率

7.几何概率

（四）空间几何部分

1.空间几何体认识

2.点.直线.平面的位置关系

3.直线.平面的平行

4.直线.平面的垂直

5.三视图，外接球问题

（五）直线与圆的方程部分

1.直线的倾斜角与斜率

2.五种直线方程形式

3.直线的位置关系

4.距离问题

5.圆的方程求法

6.点与圆的位置关系，圆与圆的位置关系

7.直线与圆的位置关系

（六）参数方程

1.参数方程的化法

2.极坐标方程的化法

3.弦长，距离，交点问题

（七）二次曲线部分

1.椭圆方程求法及离心率

2.双曲线求法及离心率与渐近线方程

3.抛物线的标准方程及性质

（八）函数专题部分

1.函数的概念，定义域和函数的求值（分段函数，对数运算为主）

2.函数的性质

3.指数与对数的运算（比较大小）

4.零点的存在性问题

5.定义域求法+导数运算

6.切线方程求法

7.导数的应用

二轮复习（2023.2月初---2023.4月初），主要是以考试和评讲试卷为主，针对性的对每个板块复习，首先是对大题部分进行复习，其次，再对小题部分进行复习，要求学生达到6--------8个小题，限时在45分钟内完成，以讲带考的形式进行，及时发现学生出现的问题，进行针对性补充教学。

三轮复习（2023.4月初到5月底）：为期7周的综合卷冲刺训练

艺术生复习进度：

上课进度：

首先是一周的试听课安排：安排数列专题进行教学：

（1）不等式的解法（单型）

（2）不等式解法（异侧双型）

（3）不等式解法（同侧双型）

（4）方程的解法：过渡下一元一次方程，分式方程，重点讲一元二次方程

（5）方程组解法：二元一次方程组，二元二次方程组解法

一轮复习：

（一）高考基础小题专题：

考点1 集合的运算

考点2 复数的运算

考点3 命题及关系

考点4 不等式解法

考点5 线性规划

考点6 流程图

考点7 平面向量

考点8 函数的图像

考点9 函数的零点

（二）基础大题专题：

一、三角函数专题

考点10 三角函数的求值（同角，诱导公式，和差倍角）

考点11 解三角形（正弦.余弦定理，面积周长问题）

考点12 三角函数的性质

考点13 三角函数图像

考点14 三角函数的平移

二.、数列专题

考点15 一般数列的通项求法

考点16 等差数列及求和

考点17 等差数列及求和

考点18 一般数列的求和

三、统计与概率专题

考点19 简单的抽样

考点20 样本估计总体（频率直方图.茎叶图）

考点21 回归方程.独立性检验

考点22 随机事件的概率

考点23 古典概率

考点24 几何概率

四、空间几何专题

考点25 点.直线.平面的位置

考点26 直线.平面的平行

考点27 直线.平面的垂直

考点28 三视图.球的问题

五、解析几何专题

考点29 直线与圆的方程

考点30 参数与极坐标

考点31 椭圆.双曲线.抛物线

六、选讲部分（函数+导数部分为主）（根据时间调整学习内容）

考点32 函数的概念与定义域

考点33 函数的性质

考点34 指数与对数

考点35 基本不等式

考点36 导数的运算

考点37 导数的几何意义（切线方程）

考点38 导数与单调性

考点39 导数与极值（最值）

考点40 轨迹方程求法

二轮复习：板块复习（八周训练）

板块一：统计与概率大题

板块二：三角函数大题

板块三：数列大题

板块四：空间几何大题首问

板块五：参数方程与极坐标.二次曲线的方程大题首问

板块六：导数大题首问

板块七：选择填空题部分

三轮复习：综合试卷冲刺（六周训练）

英语学科教学进度计划表

2022.7月--2023.6月

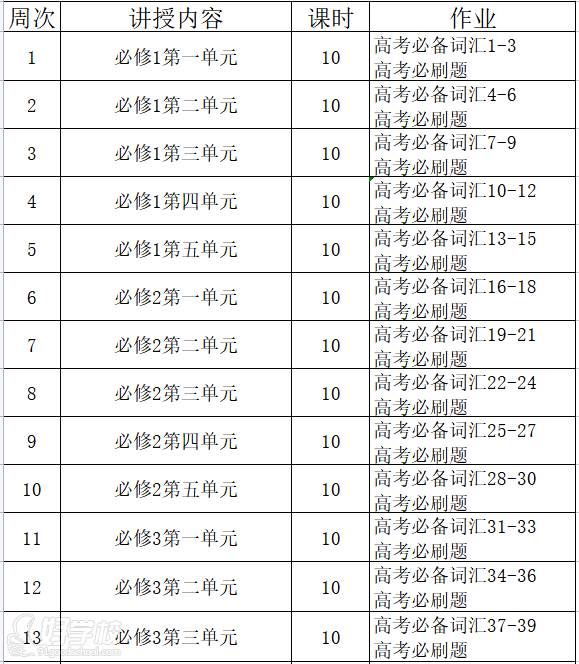
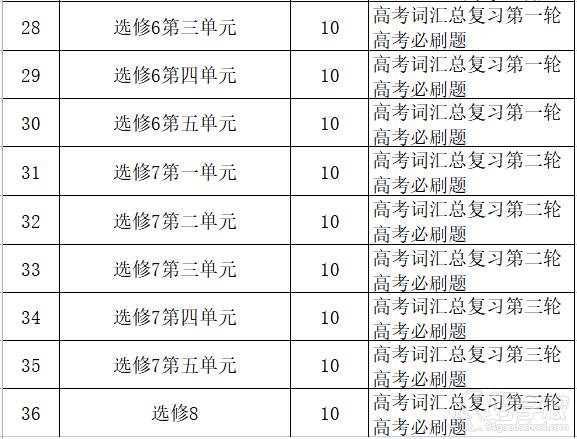
选修8时间灵活安排。高考必刷题为手写复印版，其中生词列入高考必背词汇，进度只快不慢。

【开班时间】

7月

【关于我们】

遵义启睿学校证照齐全，场地约1000平米，宽敞明亮，教学及办公设备先进。艺术类普通高考和复读集训基地可容纳500余人，环境优美，也便于封闭管理。

本校拥有一个由专家教授组成的强大教学团队，专注于高中各学科高考辅导和高中（初中、小学）数学奥赛优质辅导、高考复读以及艺术类普通高考等专业辅导。

本校进行系统化管理，根据学生的特点不断改进教学计划；坚持以生为本，为学生提供个性化教学方案和培训方式，并定期举办各学科“中学生系列讲座”，目的在于：培养学科兴趣、提升学科素养、开阔学科视野、掌握思想、方法、技巧、增强学习信心、克服畏难情绪，推动学生全面进步。另外，本校将不定期对家长举办“家庭教育系列讲座”。

本校和全国一流教育机构“新东方”、“爱学习”等具有长期合作伙伴关系，引进优秀的管理系统和教学系统及师资培训系统，使得我校的管理及教学如虎添翼。对那些以重点大学为目标的优秀学员，如果家长愿意，我们可推荐去北京参加集训。

本校努力追求“让学生没有难学的课程”，科学的教学模式以及高水平的教学专家团队能使学习困难的学生变成良好，使良好的学生变得优秀，使优秀的学生更加优秀。

让学生通过快乐学习考上自己理想的大学，这是我们努力追求的目标。

【师资】

数学老师-夏体勋

从事高三数学教学近10年，对高考有很好的研究，对每年高考的考点把握很准，每年学生高考在数学上都在近30分涨幅，2021年高考学生平均涨分40分左右。教学风格:上课活跃，对每一个知识点讲的很透彻，在教学上着重技巧和方法，让每个层次学生都可以轻松学懂，深受学生的喜爱。责任心；责任心强，对学生有足够耐心。